LUDICA.

LUDICA.
SEXTO PROMOCIÓN 2026

martes, 10 de mayo de 2016


NOVENO

Regla de Cramer

La regla de Cramer es un teorema del álgebra lineal que da la solución de un sistema lineal de ecuaciones en términos de determinantes. Recibe este nombre en honor aGabriel Cramer (1704 - 1752), quien publicó la regla en su Introduction à l'analyse des lignes courbes algébriques de 1750, aunque Colin Maclaurin también publicó el método en su Treatise of Geometry de 1748 (y probablemente sabía del método desde 1729).1
La regla de Cramer es de importancia teórica porque da una expresión explícita para la solución del sistema. Sin embargo, para sistemas de ecuaciones lineales de más de tres ecuaciones su aplicación para la resolución del mismo resulta excesivamente costosa: computacionalmente, es ineficiente para grandes matrices y por ello no es usado en aplicaciones prácticas que pueden implicar muchas ecuaciones. Sin embargo, como no es necesario pivotar matrices, es más eficiente que la eliminación gaussiana para matrices pequeñas, particularmente cuando son usadas operaciones SIMD.
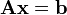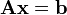Si \mathbf{Ax} = \mathbf{b} es un sistema de ecuaciones. \mathbf{A} es la matriz de coeficientes del sistema, \mathbf{x} = (x_1,\dots,x_n) es el vector columna de las incógnitas y \mathbf{b} es el vector columna de los términos independientes. Entonces la solución al sistema se presenta así:
x_j = \cfrac { \det(\mathbf{A}_j) }{ \det(\mathbf{A}) }
donde \mathbf{A}_j es la matriz resultante de reemplazar la j-ésima columna de \mathbf{A} por el vector columna \mathbf{b}. Hágase notar que para que el sistema sea compatible determinado, el determinante de la matriz \mathbf{A} ha de ser no nulo.

Índice

  [mostrar] 

Sistema de 2x2[editar]

Para la resolución de un sistema de dos ecuaciones con dos incógnitas, de la forma. Dado el sistema de ecuaciones:
a{\color{blue}x}+b{\color{blue}y} = {\color{red}e}\,
c{\color{blue}x}+d{\color{blue}y} = {\color{red}f}\,
Se representa matricialmente :
\begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} {\color{blue}x} \\ {\color{blue}y} \end{bmatrix} = \begin{bmatrix} {\color{green}e} \\ {\color{green}f} \end{bmatrix}
Entonces, x e y pueden ser encontradas con la regla de Cramer, con una división de determinantes, de la siguiente manera:
x = \frac { \begin{vmatrix} \color{red}{e} & b \\ \color{red}{f} & d \end{vmatrix} }{ \begin{vmatrix} a & b \\ c & d \end{vmatrix} } = \frac{ {\color{red} e } d - b {\color{red} f } }{ ad - bc }; \quad y = \frac { \begin{vmatrix} a & \color{red}{e} \\ c & \color{red}{f} \end{vmatrix} }{ \begin{vmatrix} a & b \\ c & d \end{vmatrix} } = \frac{ a{\color{red} f } - {\color{red} e } c }{ ad - bc }

Ejemplo[editar]

Ejemplo de la resolución de un sistema de 2x2:
Dado
3x+1y = 9\,
2x+3y = 13\,
que matricialmente es:
\begin{bmatrix} 3 & 1 \\ 2 & 3 \end{bmatrix}\begin{bmatrix} x \\ y \end{bmatrix}=\begin{bmatrix} 9 \\ 13 \end{bmatrix}
x e y pueden ser resueltos usando la regla de Cramer
x = \frac { \begin{vmatrix} 9 & 1 \\ 13 & 3 \end{vmatrix} } { \begin{vmatrix} 3 & 1 \\ 2 & 3 \end{vmatrix} } = { 9 \cdot 3 - 1 \cdot 13 \over 3 \cdot 3 - 1 \cdot 2} = 2
y = \frac { \begin{vmatrix} 3 & 9 \\ 2 & 13 \end{vmatrix} } { \begin{vmatrix} 3 & 1 \\ 2 & 3 \end{vmatrix} } = { 3 \cdot 13 - 9 \cdot 2 \over 3 \cdot 3 - 1 \cdot 2} = 3

Sistema de 3x3[editar]

La regla para un sistema de 3x3, con una división de determinantes:
\begin{cases} a{\color{blue}x} + b{\color{blue}y} + c{\color{blue}z} = {\color{black}j}\\ d{\color{blue}x} + e{\color{blue}y} + f{\color{blue}z} = {\color{black}k}\\ g{\color{blue}x} + h{\color{blue}y} + i{\color{blue}z} = {\color{black}l} \end{cases}
Que representadas en forma de matriz es:
\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \begin{bmatrix} {\color{blue}x} \\ {\color{blue}y} \\ {\color{blue}z} \end{bmatrix} = \begin{bmatrix} {\color{red}j} \\ {\color{red}k} \\ {\color{red}l} \end{bmatrix}
x, y, z pueden ser encontradas como sigue:
x = \frac { \begin{vmatrix} {\color{red}j} & b & c \\ {\color{red}k} & e & f \\ {\color{red}l} & h & i \end{vmatrix} }{ \begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix} }; \quad y = \frac { \begin{vmatrix} a & {\color{red}j} & c \\ d & {\color{red}k} & f \\ g & {\color{red}l} & i \end{vmatrix} }{ \begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix} } , \quad z = \frac { \begin{vmatrix} a & b & {\color{red}j} \\ d & e & {\color{red}k} \\ g & h & {\color{red}l} \end{vmatrix} }{ \begin{vmatrix} a & b & c \\ d & e & f \\ g & h & i \end{vmatrix} }

Ejemplo[editar]

\left\lbrace \!\!\! \begin{array}{rl} 3x+2y+1z =& \!\!\!1 \\ 2x+0y+1z =& \!\!\!2 \\ -1x+1y+2z =& \!\!\!4 \end{array} \right.
expresado en forma matricial:  \begin{bmatrix} \,\,\,\,3 & 2 & 1 \\ \,\,\,\,2 & 0 & 1 \\ -1 & 1 & 2 \end{bmatrix} \begin{bmatrix} x\\ y\\ z \end{bmatrix}= \begin{bmatrix} 1\\ 2\\ 4 \end{bmatrix}
Los valores de x, y \text{ y } z serían:
x= \frac { \begin{vmatrix} 1 & 2 & 1\\ 2 & 0 & 1\\ 4 & 1 & 2 \end{vmatrix} }{ \begin{vmatrix} \,\,\,\,3 & 2 & 1\\ \,\,\,\,2 & 0 & 1\\ -1 & 1 & 2 \end{vmatrix} } ; \quad y= \frac { \begin{vmatrix} \,\,\,\,3 & 1 & 1\\ \,\,\,\,2 & 2 & 1\\ -1 & 4 & 2 \end{vmatrix} }{ \begin{vmatrix} \,\,\,\,3 & 2 & 1\\ \,\,\,\,2 & 0 & 1\\ -1 & 1 & 2 \end{vmatrix} } ; \quad z= \frac { \begin{vmatrix} \,\,\,\,3 & 2 & 1\\ \,\,\,\,2 & 0 & 2\\ -1 & 1 & 4 \end{vmatrix} }{ \begin{vmatrix} \,\,\,\,3 & 2 & 1\\ \,\,\,\,2 & 0 & 1\\ -1 & 1 & 2 \end{vmatrix} }
Publicado por en

9 comentarios:

  1. Tecnologías De La Ofimática13 de mayo de 2016, 11:16

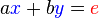
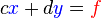
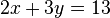
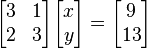
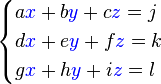
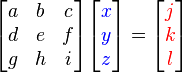
    con esta lectura nos que dan las cosa mas claras

    ResponderEliminar
  2. Unknown13 de mayo de 2016, 11:26

    esta información esta muy concreta
    gracias profe por que nos facilita las matematicas

    ResponderEliminar
  3. Unknown13 de mayo de 2016, 11:27

    LA LECTURA ESTA MUY INTERESANTE YA QUE PODEMOS APRENDER MUCHO MAS MATEMATICAS

    ResponderEliminar
  4. Unknown13 de mayo de 2016, 12:28

    excelente articulo

    ResponderEliminar
  5. Unknown24 de mayo de 2016, 7:22

    interesante articulo nos facilitara el desempeño en el tema

    ResponderEliminar
  6. Unknown24 de mayo de 2016, 7:22

    interesante articulo nos facilitara el desempeño en el tema

    ResponderEliminar
  7. Unknown2 de junio de 2016, 10:58

    uy profe este tema esta muy facil y entendible

    ResponderEliminar
  8. Unknown19 de julio de 2016, 6:31

    Entendi perfectamente el tema ...!! El manejo del tema fue mas complejo ya que con base en este articulo podemos tener conocimiento mas profundo del tema ...!!

    ResponderEliminar
  9. jorge alexander alarcon24 de agosto de 2016, 11:55

    Muy bueno porque hay lectura

    ResponderEliminar

Suscribirse a: Enviar comentarios (Atom)